При выборе формата листа (картины) на практике часто прибегают к использованию «классических» пропорций сторон прямоугольника, где соотношение меньшей стороны к большей составляет число 0,6180339, а отношение большей стороны к меньшей — 1,6180339. Это принцип также известен как «золотое сечение прямоугольника».
Основа учения о гармонии мира, выраженная в числовых отношениях, была заложена древнегреческим учёным-математиком Пифагором (VI в до н.э). Им представлено золотое сечение как одна из закономерностей, математически точно определяющая наиболее красивое и гармоничное соотношение частей целого, разделённого на две неравные половины.
На соотношении частей отрезка в пропорциях золотого сечения основано построение прямоугольника. С помощью диагоналей осуществляется членение его на составные части, при котором образуется динамика пропорциональных фигур — квадрата, прямоугольника, а также прямоугольного и равнобедренного треугольников.
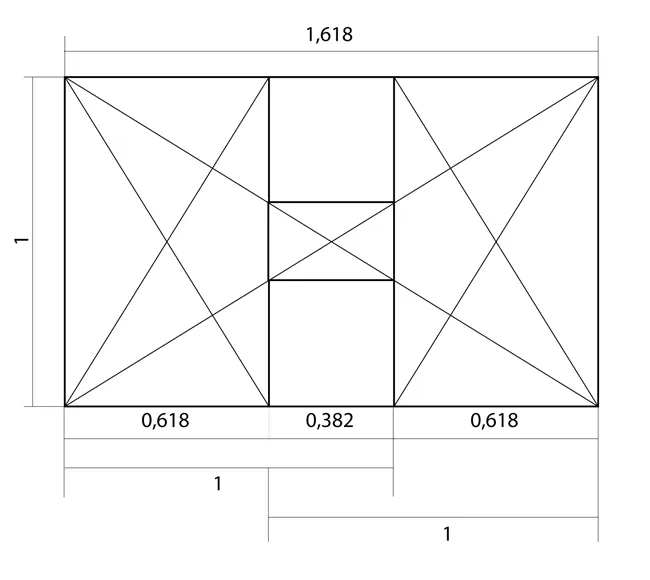
Т.о., используя диагонали можно получить последовательный ряд увеличивающихся прямоугольников, с соотношением сторон — 1:√ 2, 1:√3, 1:√4, 1:√5, производных от квадрата.
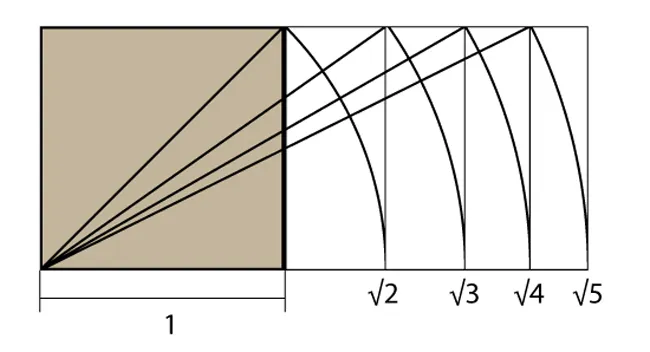
При стороне √4 образуется прямоугольник с удвоенным квадратом. При стороне √3 образуется два прямоугольных треугольника, у которых общая гипотенуза является диагональю прямоугольника, равная удвоенной величине меньшего катета (т.е. стороне квадрата), и они имеют острые углы 30 и 60 градусов.
Диагональ используется и в построении последовательно увеличивающихся квадратов, создающих «динамическое» развитие их величины.
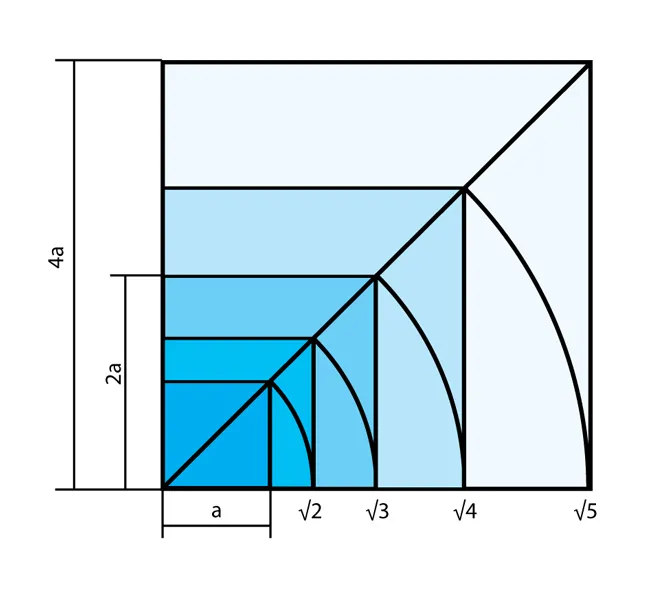
В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне. Эти преобразования иногда называют «активным квадратом».
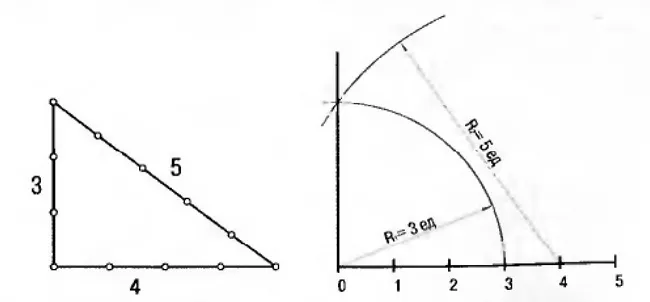
Геометрическая система динамических пропорций квадрата, прямоугольника и треугольника были основой в создании архитектурных сооружений в ранний период Древнего Египта. Кроме того, в условиях примитивной техники архитектурного строительства в те далёкие времена постоянно требовалось восстановление перпендикуляра к прямой, которое осуществлялось тогда при помощи верёвки с 12 узлами. С использованием такого приспособления получался прямоугольный треугольник с отношением строно — 3:4:5, который впоследствии стали называть египетским. В настоящее время на его основе строят прямые углы и проводят перпендикуляры к концу отрезка.
С древнейших времён золотое сечение используется в практике построения различных изображений. Это способствует созданию гармоничных образов и уравновешенности пропорций во всём, что на окружает. Пропорции золотого сечения присутствуют в мамематике, и особенно в геометрии, в изобразительном искусстве, в быту и в природе, в растительном и животном мире.
Золотое сечение получило широкое развитие в математике. Так, в XVI веке итальянский учёный Фибоначчи выстроил математический ряд цифр, при котором последующее число определяет сумму двух предыдущих — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Кроме того, устанавливается и другая зависимость этих чисел, при которой отношение каждого последующего к предыдущему выражается числом 1,618…, а предыдущего к последующему — 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
Особенно часто золотое сечение используется в геометрии при делении окружности на равные части и построении правильных многоугольников.
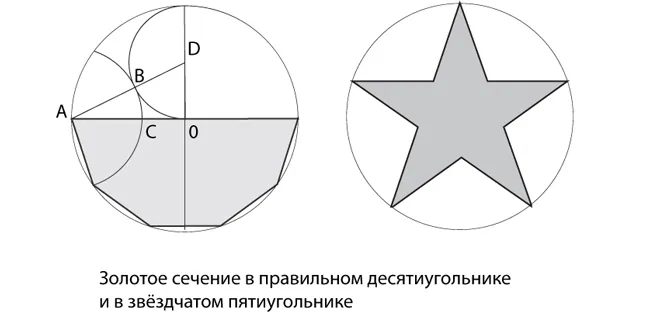
В звёздчатом многоугольнике — пятиконечной звезде, каждая точка пересечения её сторон делит их на две неравные части в пропорциях золотого сечения.
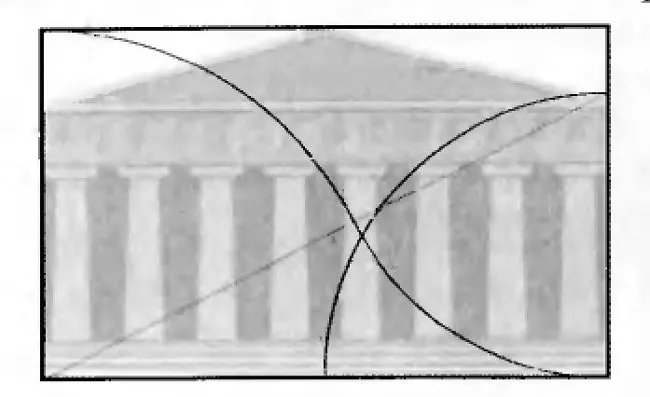
С древнейших времён золотое сечение применялось в различных видах изобразительного искусства — в архитектуре, вкульптуре, живописи. Парфенон — классический пример применения золотого сечения в архитектуре.
Особенно широко использовал в своём творчестве соотношение величин золотого сечения Леонардо да Винчи, которое он назвал «божественная пропорция».
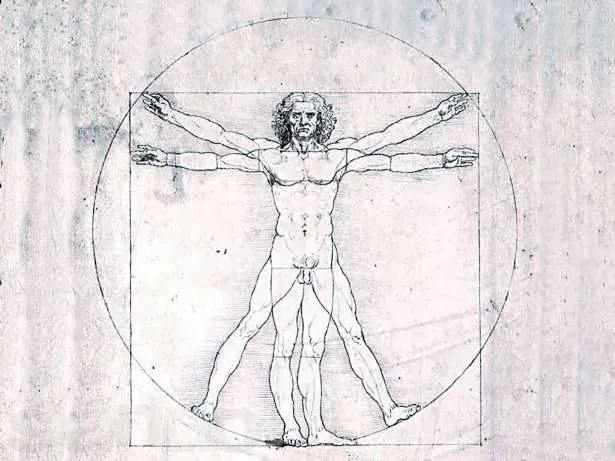
Числовой гармонии золотого сечения подчиняются также античные статуи греческого искусства, отражающие пропорции идеально сложённого человеческого тела.
Золотое сечение применяют в начертании букв и цифр различного шрифта.
Золотое сечение часто используют в определении величины прямоугольника при заданной его большей или меньшей стороне. Если у прямоугольной картины задана длина (АВ), то её высоту (АС) определяют следующим построением:
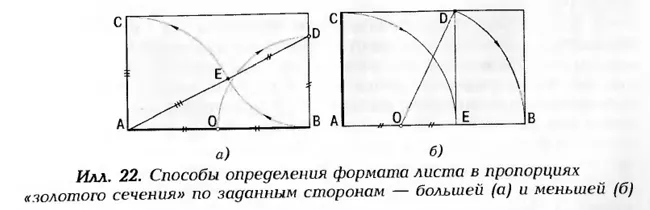
Сначала из конца отрезка (В) проводят дугу, равную его половине до пересечения с перпендикуляром (АО=ОВ=ВД). Полученную точку Д соединяют прямой с другим концом отрезка (А). Затем из точки Д проводят дугу радиусом ВД до пересечения с этой прямой и отмечают точку Е. Дуга, проведённая из конца отрезка А радиусом АЕ определяет по вертикальной прямой точку С и искомую высоту картины АС.
Если задана высота картины (АС), то её длину (АВ) определяют другим построением. Сначала строят квадрат АСДЕ со стороной равной АС. Затем из середины стороны квадрата (О) проводят дугу радиусом ОД и получают на горизонтальной прямой точку В, которая определит искомую длину стороны прямоугольной картины АВ.
По прямоугольнику с золотыми пропорциями можно построить любой величинны подобный формат листа.
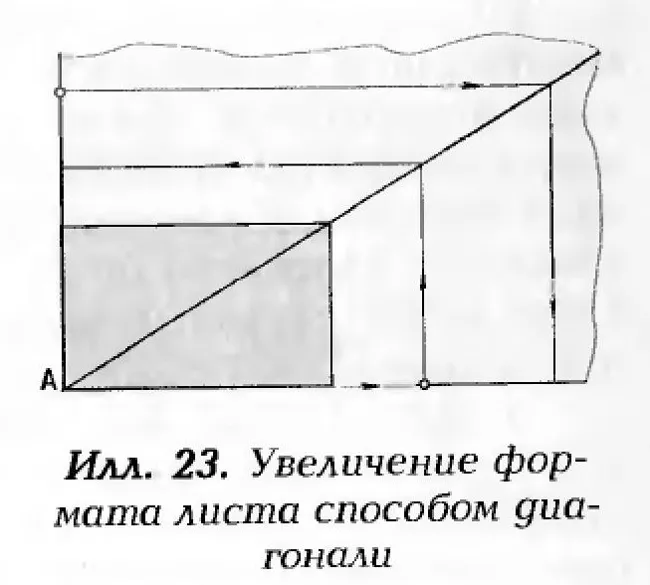
Для этого его накладывают на лист бумаги в один из его углов (А) и проводят в нём диагональ. Затем от точки А откладывают заданный размер горизонтальной или вертикальной стороны формата листа и через его конец проводят перпендикуляр до пересечения с диагональю, которая определит вторую сторону прямоугольника.
Источник: М.Н. Макарова «Практическая перспектива»
Как правильно построить золотое сечение?
Золотое сечение — это математическое соотношение, которое определяется как отношение двух отрезков в таком порядке, что отношение большего отрезка ко всей линии равно отношению меньшего отрезка к большему отрезку. Оно обозначается греческой буквой φ (фи) и имеет приблизительное значение 1,618.
Существует несколько способов построения золотого сечения:
-
Метод деления отрезка: Возьмите отрезок любой длины и разделите его на две части так, чтобы соотношение меньшей части к большей было равно золотому сечению.
-
Метод деления окружности: Нарисуйте окружность и поставьте на ней две точки так, чтобы расстояние между ними было равно диаметру окружности. Соедините эти точки дугой и проведите на ней перпендикуляр к диаметру. Точка пересечения перпендикуляра и дуги будет делить ее на две части в соотношении золотого сечения.
-
Метод построения прямоугольника: Нарисуйте прямоугольник со сторонами в соотношении золотого сечения. Затем проведите диагонали прямоугольника. Точка пересечения диагоналей будет находиться на расстоянии, равном золотому сечению от каждого из углов прямоугольника.
Эти методы могут быть использованы для построения фигур, которые соответствуют золотому сечению, таких как золотой прямоугольник или золотой треугольник.
