Добавлено 13 января 2021 в 05:06
Давайте проведем анализ простой последовательной схемы и определим падение напряжения на каждом из резисторов. Исходя из предоставленных значений сопротивлений, мы можем вычислить общее сопротивление цепи, учитывая, что последовательные резисторы складываются. Таким образом, мы можем выполнить расчет напряжения по делителю напряжения.
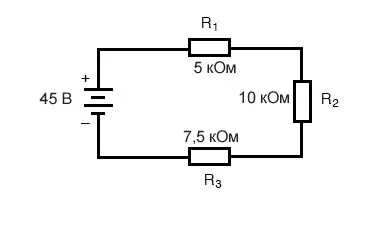Рисунок 1 – Схема последовательной цепи
Рисунок 2 – Табличный метод. Шаг 1
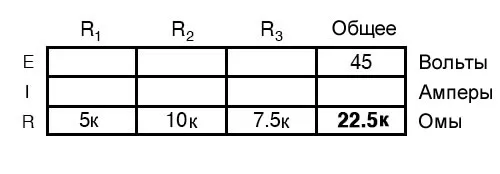Рисунок 3 – Табличный метод. Шаг 2Теперь мы можем использовать закон Ома (I = E/R) для определения общего тока, который, как мы знаем, будет таким же, как ток каждого резистора, поскольку токи во всех частях последовательной цепи одинаковы.
Рисунок 4 – Табличный метод. Шаг 3Теперь, зная, что ток в цепи равен 2 мА, мы можем использовать закон Ома (E = IR) для расчета напряжения на каждом резисторе:
Рисунок 5 – Табличный метод. Шаг 4Должно быть очевидно, что падение напряжения на каждом резисторе пропорционально его сопротивлению, учитывая, что ток одинаков на всех резисторах. Обратите внимание, что напряжение на R2 вдвое больше, чем на R1, так же как сопротивление R2 в два раза больше, чем у R1.
Если бы мы изменили общее напряжение, то обнаружили бы, что эта пропорциональность падений напряжения остается постоянной.
Рисунок 6 – Пропорциональность падений напряжения остается постояннойНесмотря на то, что напряжение источника изменилось, напряжение на R2 по-прежнему ровно вдвое больше, чем на R1. Пропорциональность падений напряжения (соотношение между ними) строго зависит от значений сопротивлений.
При более внимательном наблюдении становится очевидным, что падение напряжения на каждом резисторе также является фиксированной долей напряжения питания. Например, напряжение на R1 составляло 10 вольт при питании от батареи 45 вольт. Когда напряжение аккумулятора было увеличено до 180 вольт (в 4 раза больше), падение напряжения на R1 также увеличилось в 4 раза (с 10 до 40 вольт). Однако соотношение между падением напряжения R1 и общим напряжением не изменилось:
\[\frac{E_{R1}}{E_{общ}} = \frac{10 \ В}{45 \ В} = \frac{40 \ В}{180 \ В} = 0,22222\]
Точно так же ни один из других коэффициентов падения напряжения не изменился с увеличением напряжения питания:
\[\frac{E_{R2}}{E_{общ}} = \frac{20 \ В}{45 \ В} = \frac{80 \ В}{180 \ В} = 0,44444\]
\[\frac{E_{R3}}{E_{общ}} = \frac{15 \ В}{45 \ В} = \frac{60 \ В}{180 \ В} = 0,33333\]
Формула делителя напряжения
По этой причине последовательную цепь часто называют делителем напряжения из-за ее способности пропорционально делить общее напряжение на дробные части с постоянными коэффициентами. Применив немного алгебры, мы можем вывести формулу для определения падения напряжения на последовательном резисторе, не учитывая ничего, кроме общего напряжения, сопротивления отдельного резистора и общего сопротивления.
Падение напряжения на любом резисторе:
\[E_n = I_n R_n\]
Сила тока в последовательной цепи:
\[I_{общ} = \frac{E_{общ}}{R_{общ}}\]
Подставляем Eобщ/Rобщ вместо In в первую формулу…
Падение напряжения на любом резисторе в последовательнй цепи:
\[E_n = \frac{E_{общ}}{R_{общ}} R_n\]
или
\[\large E_n = \frac{R_n}{R_{общ}} E_{общ}\]
В схеме делителя напряжения отношение отдельного сопротивления к общему сопротивлению равно отношению отдельного падения напряжения к общему напряжению питания. Эта формула известна как формула делителя напряжения, и это сокращенный метод определения падения напряжения в последовательной цепи без проведения расчетов тока по закону Ома.
Пример использования формулы делителя напряжения
Используя эту формулу, мы можем повторно проанализировать падение напряжения в примере схемы за меньшее количество шагов:
Рисунок 7 – Схема последовательной цепи\[E_{R1} = 45 \ В \ \frac{5 \ кОм}{22,5 \ кОм} = 10 В\]
\[E_{R2} = 45 \ В \ \frac{10 \ кОм}{22,5 \ кОм} = 20 В\]
\[E_{R3} = 45 \ В \ \frac{7,5 \ кОм}{22,5 \ кОм} = 15 В\]
Компоненты, делящие напряжение
Делители напряжения находят широкое применение в измерительных схемах, где как часть схемы измерения напряжения для «деления» напряжения на точные пропорции используются определенные комбинации последовательных резисторов.
Рисунок 8 – Делитель напряженияПотенциометры как компоненты, делящие напряжение
Одним из устройств, часто используемых в качестве элемента деления напряжения, является потенциометр, который представляет собой резистор с подвижным элементом, перемещаемым ручкой или рычагом. Подвижный элемент, обычно называемый ползунком, вступает в контакт с резистивной полосой материала в любой, выбранной вручную точке:
Рисунок 9 – ПотенциометрКонтакт ползунка – это обращенная влево стрелка, нарисованная в середине вертикального обозначения резистора. При перемещении вверх он контактирует с резистивной полосой ближе к клемме 1 и дальше от клеммы 2, уменьшая сопротивление от него до клеммы 1 и повышая сопротивление от него до клеммы 2. При перемещении вниз происходит противоположный эффект. Сопротивление, измеренное между клеммами 1 и 2, постоянно для любого положения ползунка.
Рисунок 10 – Принцип действия потенциометраПоворотные и линейные потенциометры
Ниже показано внутреннее устройство двух типов потенциометров: поворотного и линейного.
Линейные потенциометры
Рисунок 11 – Конструкция линейного потенциометраНекоторые линейные потенциометры приводятся в действие прямолинейным движением рычага или ползунковой кнопки. Другие, подобные изображенному на рисунке выше, приводятся в действие поворотным винтом для точной регулировки. Потенциометры последнего типа иногда называют «подстроечниками» потому, что они хорошо работают в приложениях, требующих «подстройки» переменного сопротивления до некоторого точного значения.
Следует отметить, что не все линейные потенциометры имеют такое же назначение выводов, как показано на этом рисунке. У некоторых вывод ползунка находится посередине между двумя крайними выводами.
Поворотный потенциометр
На изображении ниже показана конструкция поворотного потенциометра.
Рисунок 12 – Поворотный потенциометрНа фотографии ниже показан реальный поворотный потенциометр с открытыми для удобства просмотра ползунком и резистивным элементом. Вал, который перемещает ползунок, повернут почти до конца по часовой стрелке, поэтому ползунок почти касается левого конечного вывода резистивного элемента:
Рисунок 13 – Поворотный потенциометр с открытыми ползунком и резистивным элементомВот тот же потенциометр с валом ползунка, перемещенным почти до упора против часовой стрелки, поэтому ползунок теперь находится рядом с другим крайним концом хода:
Рисунок 14 – Потенциометр с валом ползунка, повернутым до упора против часовой стрелкиВлияние регулировки потенциометра на схему
Если между внешними выводами (по всей длине резистивного элемента) приложено постоянное напряжение, положение ползунка будет отводить часть приложенного напряжения, измеряемого между контактом ползунка и любым из двух других выводов. Значение коэффициента деления полностью зависит от физического положения ползунка:
Рисунок 15 – Потенциометр как переменный делитель напряженияВажность потенциометров
Как и в случае с фиксированным делителем напряжения, коэффициент деления напряжения потенциометра строго зависит от сопротивления, а не от величины приложенного напряжения. Другими словами, если ручка потенциометра или рычаг перемещается в положение 50 процентов (точное центральное положение), падение напряжения между ползунком и любым крайним выводом будет составлять ровно 1/2 от приложенного напряжения, независимо от того, что с этим напряжением происходит, или каково полное сопротивление потенциометра. Другими словами, потенциометр работает как регулируемый делитель напряжения, где коэффициент деления напряжения устанавливается положением ползунка.
Это применение потенциометра является очень полезным средством получения изменяемого напряжения от источника фиксированного напряжения, такого как аккумулятор. Если для схемы, которую вы собираете, требуется определенная величина напряжения, которая меньше, чем значение напряжения доступной батареи, вы можете подключить внешние выводы потенциометра к этой батарее и «выбрать» для использования в вашей цепи любое необходимое напряжение между ползунком и одним из внешних выводов потенциометра:
Рисунок 16 – Применение потенциометраПри таком использовании название «потенциометр» имеет смысл: он «измеряет» (контролирует) приложенный к нему потенциал (напряжение), создавая изменяемый коэффициент деления напряжения. Такое использование трехполюсного потенциометра в качестве переменного делителя напряжения очень популярно в схемотехнике.
Примеры небольших потенциометров
Ниже показано несколько небольших потенциометров, которые обычно используются в бытовом электронном оборудовании, а также любителями и студентами при построении схем:
Рисунок 17 – Примеры небольших потенциометровМеньшие устройства слева и справа предназначены для подключения к беспаечной макетной плате или для пайки в печатную плату. Устройства посередине предназначены для установки на плоской панели с проводами, припаянными к каждому из трех выводов.
Ниже показано еще три потенциометра, более специализированных, чем только что показанный набор:
Рисунок 18 – Примеры потенциометров размером побольшеБольшое устройство «Helipot» – это лабораторный потенциометр, предназначенный для быстрого и легкого подключения к цепи. Устройство в нижнем левом углу фотографии представляет собой потенциометр того же типа, только без корпуса и поворотного счетного диска. Оба этих потенциометра представляют собой прецизионные устройства, в которых используются многооборотные спиралевидные резистивные ленты и ползунковые механизмы для точной регулировки. Устройство в правом нижнем углу представляет собой потенциометр для монтажа на панели, предназначенный для работы в тяжелых промышленных условиях.
Резюме
- Последовательные цепи делят общее напряжение питания на отдельные падения напряжения, коэффициенты деления строго зависят от сопротивлений: ERn = Eобщ(Rn/Rобщ)
- Потенциометр – это элемент переменного сопротивления с тремя точками подключения, часто используемый в качестве регулируемого делителя напряжения.
Теги
Делитель напряженияДля начинающихЗакон ОмаОбучениеПоследовательная цепьПотенциометрСхемотехника
В чем разница между линейным и фазным напряжением?
Линейное напряжение и фазное напряжение относятся к электрическим системам, в которых используется трехфазное переменное напряжение.
Линейное напряжение (U<sub>л</sub>) является разностью потенциалов между любыми двумя фазами в трехфазной системе. В трехфазной системе линейное напряжение можно вычислить по формуле:
U<sub>л</sub> = √3 * U<sub>ф</sub>,
где U<sub>ф</sub> — фазное напряжение.
Фазное напряжение (U<sub>ф</sub>) — это потенциал между любой фазой и нулевой точкой в трехфазной системе.
Разница между линейным и фазным напряжением заключается в том, что линейное напряжение является напряжением между фазами, а фазное напряжение является напряжением между фазой и нулевой точкой. Фазное напряжение используется для расчета мощности однофазной нагрузки, а линейное напряжение используется для расчета мощности трехфазной нагрузки.
