Делитель напряжения представляет собой электрическую цепь, включающую два или более пассивных радиоэлемента, которые соединены последовательно. Давайте рассмотрим базовый пример расчета делителя напряжения, включающего два резистора.
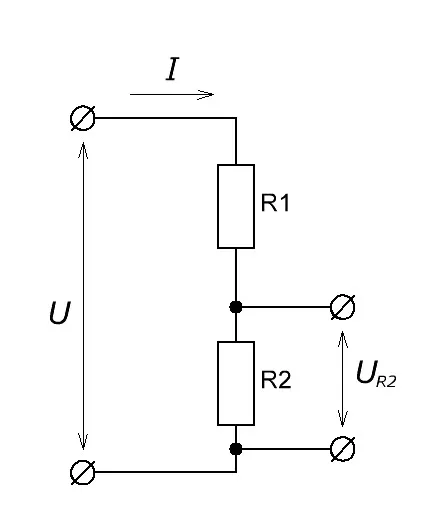
Делитель напряжения на резисторах
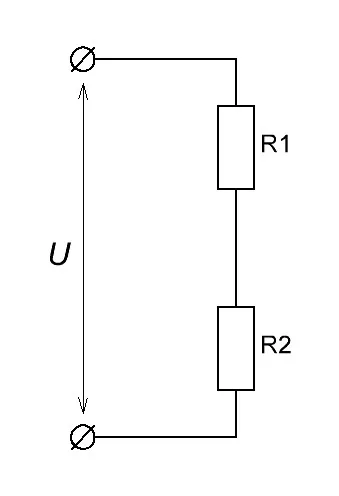
Подавая напряжение на эту цепь, состоящую из двух резисторов, у нас получается, что цепь становится замкнутой, и в цепи начинает течь электрический ток с какой-то определенной силой тока, которая зависит от номиналов резисторов.
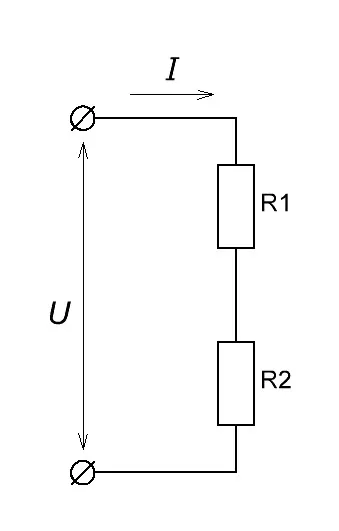
Итак, мы знаем, что при последовательном соединении сила тока в цепи одинакова. То есть какая сила тока протекает через резистор R1, такая же сила тока течет и через резистор R2. Как же вычислить эту силу тока? Оказывается, достаточно просто, используя закон Ома: I=U/R.
Так как наши резисторы соединены последовательно, то и их общее сопротивление будет выражаться формулой
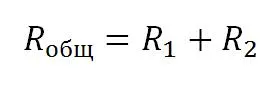
То есть в нашем случае мы можем записать, что
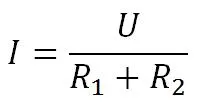
Как найти напряжение, которое падает на резисторе R2?
Так как ток для обоих резисторов общий, то согласно закону Ома
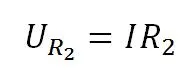
Подставляем вместо I формулу
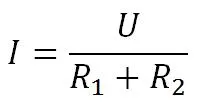
и получаем в итоге
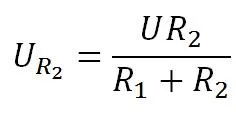
Для другого резистора ситуация аналогичная. На нем падает напряжение
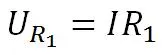
Для него формула запишется
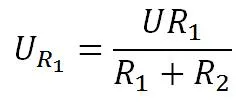
Давайте докажем, что сумма падений напряжений на резисторах равняется напряжению питания, то есть нам надо доказать, что U=UR1 +UR2 . Подставляем значения и смотрим.
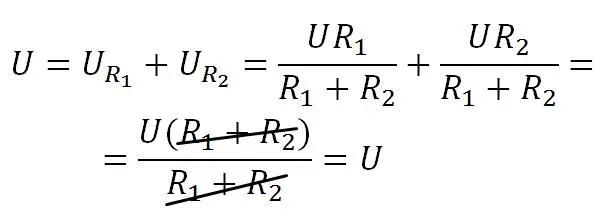
что и требовалось доказать.
Эта формула также работает и для большого количества резисторов.
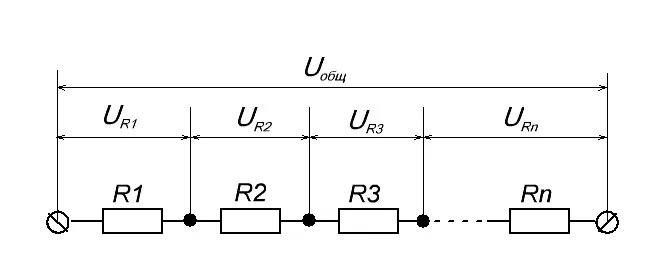
На схеме выше мы видим резисторы, которые соединены последовательно. Чему будет равняться Uобщ ? Так как резисторы соединены последовательно, следовательно, на каждом резисторе падает какое-то напряжение. Сумма падений напряжения на всех резисторах будет равняться Uобщ . В нашем случае формула запишется как
![]()
Как работает делитель напряжения на практике
Итак у нас имеются вот такие два резистора и наш любимый мультиметр:

Замеряем сопротивление маленького резистора, R1=109,7 Ом.

Замеряем сопротивление большого резистора R2=52,8 Ом.

Выставляем на блоке питания ровно 10 Вольт. Замер напряжения производим с помощью мультиметра.

Цепляемся блоком питания за эти два резистора, запаянные последовательно. Напомню, что на блоке ровно 10 Вольт. Показания амперметра на блоке питания тоже немного неточны. Силу тока мы будем замерять в дальнейшем также с помощью мультиметра.

Замеряем падение напряжения на большом резисторе, который обладает номиналом в 52,8 Ом. Мультиметр намерял 3,21 Вольта.

Замеряем напряжение на маленьком резисторе номиналом в 109,7 Ом. На нем падает напряжение 6,77 Вольт.

Ну что, с математикой, думаю, у всех в порядке. Складываем эти два значения напряжения. 3,21+6,77 = 9,98 Вольт. А куда делись еще 0,02 Вольта? Спишем на погрешность щупов и средств измерений. Вот наглядный пример того, что мы смогли разделить напряжение на два разных напряжения. Мы еще раз убедились, что сумма падений напряжений на каждом резистора равняется напряжению питания, которое подается на эту цепь.
[quads id=1]
Сила тока в цепи при последовательном соединении резисторов
Давайте убедимся, что сила тока при последовательном соединении резисторов везде одинакова. Как измерить силу тока постоянного напряжения, я писал здесь. Как видим, мультиметр показал значение 0,04 А или 40 мА в начале цепи, в середине цепи и даже в конце цепи. Где бы мы не обрывали нашу цепь, везде одно и то же значение силы тока.



Переменный резистор в роли делителя напряжения
Для того, чтобы плавно регулировать выходное напряжение, у нас есть переменный резистор в роли делителя напряжения. Его еще также называют потенциометром.

Его обозначение на схеме выглядит вот так:
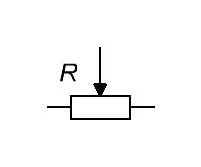
Принцип работы такой: между двумя крайними контактами постоянное сопротивление. Сопротивление относительно среднего контакта по отношению к крайним может меняться в зависимости от того, куда мы будем крутить крутилку этого переменного резистора. Этот резистор рассчитан на мощность 1Вт и имеет полное сопротивление 330 Ом. Давайте посмотрим, как он будет делить напряжение.
Так как мощность небольшая, всего 1 Вт, то мы не будем нагружать его большим напряжением. Мощность, выделяемая на каком-либо резисторе рассчитывается по формуле P=I2R. Значит, этот переменный резистор может делить только маленькое напряжение при маленьком сопротивлении нагрузки и наоборот. Главное, чтобы значение мощности этого резистора не вышло за грани. Поэтому я буду делить напряжение в 1 Вольт.
Для этого выставляем на блоке напряжение в 1 Вольт и цепляемся к нашему резистору по двум крайним контактам.

Крутим крутилку в каком-нибудь произвольном направлении и останавливаем ее. Замеряем напряжение между левым и средним контактом и получаем 0,34 Вольта.

Замеряем напряжение между средним и правым контактом и получаем 0,64 Вольта

Суммируем напряжение и получаем 0,34+0,64=0,98 Вольт. 0,02 Вольта опять где-то затерялись. Скорее всего на щупах, так как они тоже обладают сопротивлением. Как вы видите, простой переменный резистор мы можем использовать в роли простейшего делителя напряжения.
Похожие статьи по теме «делитель напряжения»
Делитель тока
Что такое резистор
Что такое напряжение
Блок питания
В чем разница между линейным и фазным напряжением?
Линейное напряжение и фазное напряжение относятся к электрическим системам, в которых используется трехфазное переменное напряжение.
Линейное напряжение (U<sub>л</sub>) является разностью потенциалов между любыми двумя фазами в трехфазной системе. В трехфазной системе линейное напряжение можно вычислить по формуле:
U<sub>л</sub> = √3 * U<sub>ф</sub>,
где U<sub>ф</sub> — фазное напряжение.
Фазное напряжение (U<sub>ф</sub>) — это потенциал между любой фазой и нулевой точкой в трехфазной системе.
Разница между линейным и фазным напряжением заключается в том, что линейное напряжение является напряжением между фазами, а фазное напряжение является напряжением между фазой и нулевой точкой. Фазное напряжение используется для расчета мощности однофазной нагрузки, а линейное напряжение используется для расчета мощности трехфазной нагрузки.
