В инженерной и строительной практике часто возникают задачи, связанные с вычислением площади поперечного сечения. Если провести разрез фигуры по линии, перпендикулярной продольной оси объекта, полученная поверхность будет представлять поперечное сечение. Если актуально, то в новом тексте будет включена «поперечное сечение формула».
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
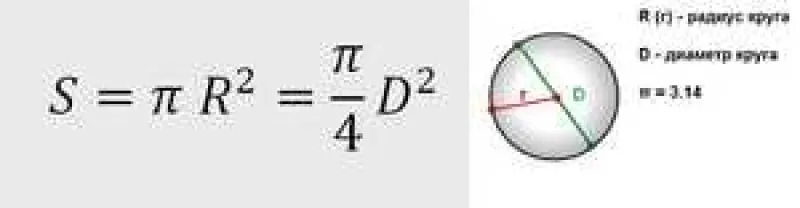
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D ) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l) .

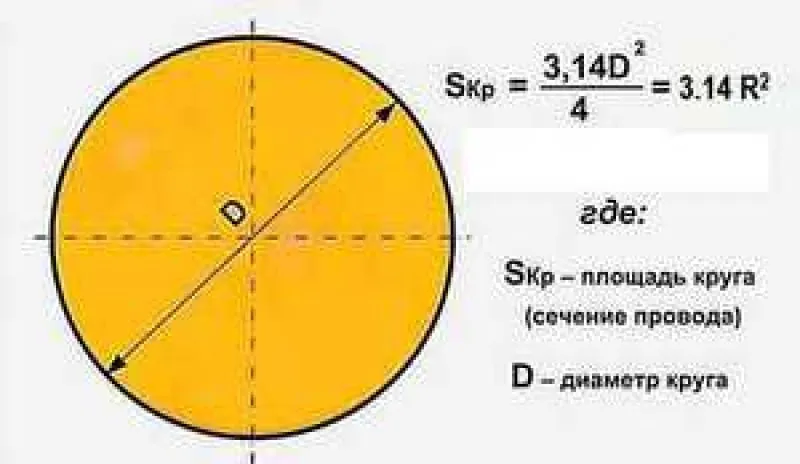
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
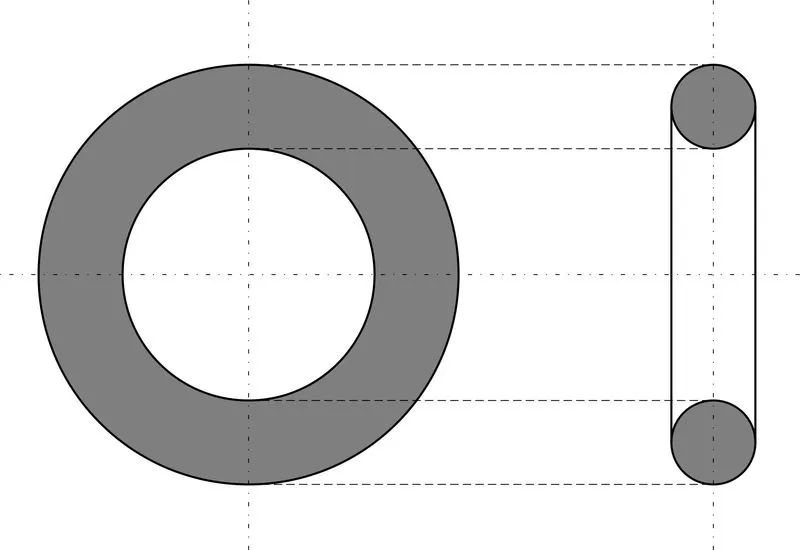
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Как самому определить сечение провода?
Для определения сечения провода вам понадобятся следующие инструменты:
- Линейка или мерная лента.
- Измерительный прибор (например, мультиметр).
- Калькулятор.
Шаги для определения сечения провода:
-
Измерьте диаметр провода. Это можно сделать с помощью линейки или мерной ленты.
-
Вычислите площадь поперечного сечения провода. Для этого используйте формулу для площади круга: S = πr², где r — радиус провода (половина его диаметра), а π — постоянная, равная приблизительно 3,14.
-
Определите материал провода (медь или алюминий) и найдите соответствующее значение сопротивления провода в таблице.
-
Используя измерительный прибор, измерьте сопротивление провода и запишите результат.
-
Используя формулу для расчета сопротивления провода R = ρL / S, где ρ — удельное сопротивление материала провода, L — длина провода, а S — площадь поперечного сечения провода, найдите длину провода.
-
Используя найденные значения сопротивления и длины провода, найдите значение ρ, удельного сопротивления материала провода, с помощью формулы ρ = RS / L.
-
Найдите необходимое сечение провода для данной нагрузки, используя таблицу, в которой указаны максимальные токи для разных сечений провода при заданных условиях.
Эти шаги помогут вам определить сечение провода для различных условий нагрузки и длины провода. Однако, для более точного результата рекомендуется проконсультироваться с профессиональным электриком, особенно если вы планируете проводить работы по электропроводке в своем доме или офисе.
