Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
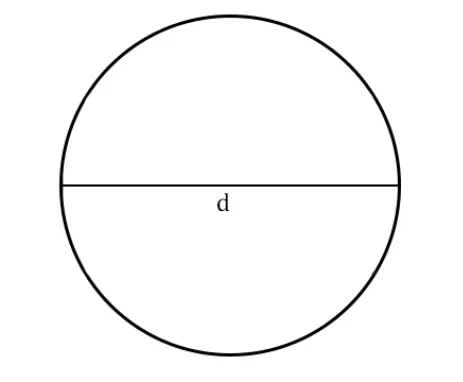
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как обозначается длина окружности?
Длина окружности обозначается буквой
.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как найти длину окружности через радиус
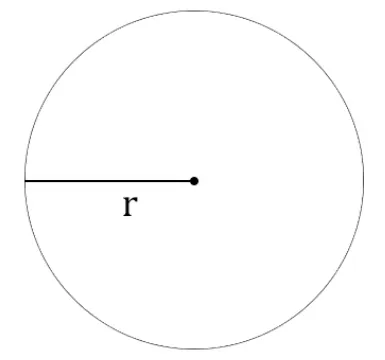
Радиус окружности представляет собой отрезок, соединяющий центр данной окружности с точкой на её границе. Формула для вычисления длины окружности через радиус следующая:Эти две ключевые формулы позволяют определить длину окружности.
l=2πr , где
π — число пи, примерно равное 3,14
r — радиус окружности
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
, где
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
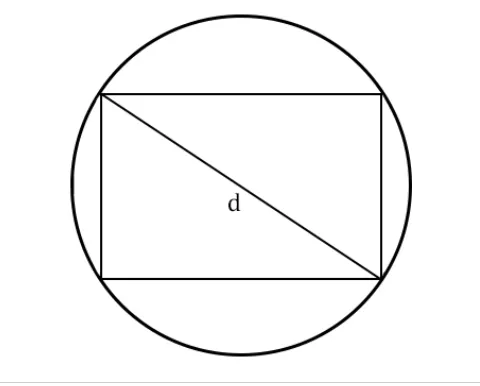
l=πd, где
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
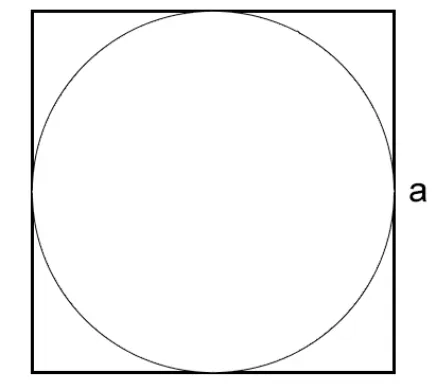
l=πa, где
π — математическая константа, примерно равная 3,14
a — сторона квадрата
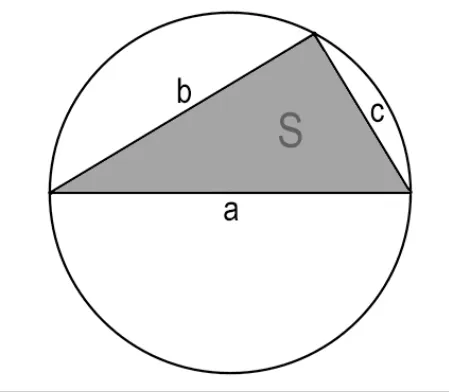
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
, где
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
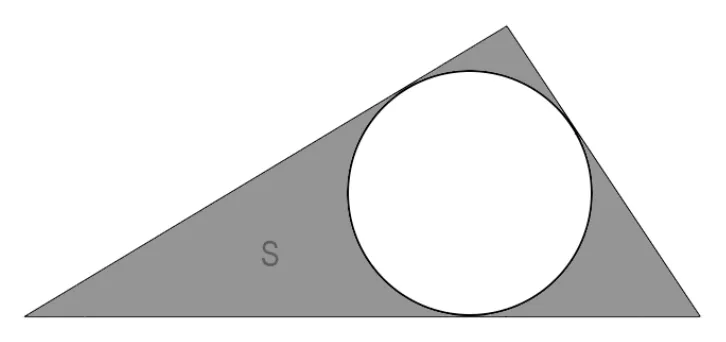
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
, где
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
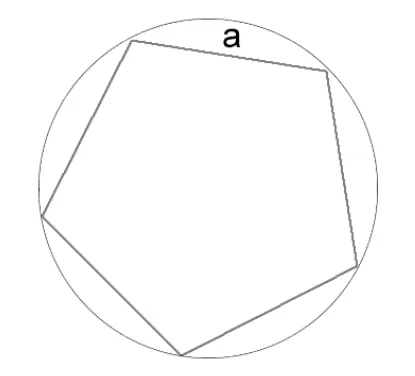
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
, где
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
(см)
Ответ: 15,7 (см)
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною дм
Решение. Радиус окружности равен . Подставим туда наши переменные и получим (дм).
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус , мы можем подставить наши данные и получить решение задачи.
Так и сделаем:
(дм)
Ответ: (дм)
Как вычислить окружность?
Окружность — это геометрическая фигура, которая состоит из всех точек на плоскости, находящихся на одном и том же расстоянии от фиксированной точки, называемой центром окружности.
Для вычисления окружности нужно знать ее радиус (расстояние от центра окружности до любой точки на окружности) или диаметр (расстояние между двумя точками на окружности через ее центр).
Для вычисления окружности по радиусу нужно умножить диаметр на число π (пи), которое равно примерно 3,14 или 22/7.
Формула для вычисления окружности: C = 2πr, где С — длина окружности, r — радиус окружности, π — число пи (примерно 3,14).
Для примера, если радиус окружности равен 5 см, то ее длина будет C = 2πr = 2 * 3,14 * 5 = 31,4 см. Таким образом, длина окружности равна 31,4 см.
Видео. КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 класс
