Вычисление длины окружности — основные аспекты и методы - «Мега Мастер»

Дом 22.09.2023

C с диаметром D, радиусом R и центром O. Circumference = × D = 2 × × R.

— это длина замкнутой плоской кривой, ограничивающей круг. Поскольку окружность является границей круга, или диска, длина окружности является частным случаем периметра[1][2]. Периметр — общая длина границы фигуры.

Круг[править | править код]

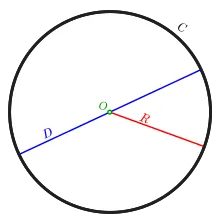
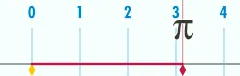
может быть определена как предел последовательности периметров вписанных в круг правильных многоугольников[3]. Термин «длина окружности» применяется при измерении физических объектов, а также при анализе абстрактных геометрических фигур. Можно выразить его как отношение длины окружности к удвоенному значению её радиуса. Это соотношение можно представить в виде следующей формулы: $\pi$ $\pi$

Если диаметр окружности равен 1, её длина равна $\pi$ .

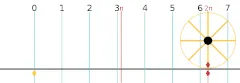
Если радиус окружности равен 1, её длина равна $2\pi$ .

и число пи[править | править код]

связана с одной из самых важных математических констант — числом пи. Число пи обозначается греческой буквой пи ( $\pi$ ). Первые цифры числа в десятичной записи — 3.141592653589793 …[4] Пи определяется как отношение длины окружности к её диаметру :

$\pi ={\frac {C}{d}}$

${C}=\pi \cdot {d}=2\pi \cdot {r}.\!$

Использование константы $\pi$ является повсеместным в науке и приложениях.

В книге «Измерение круга[en]», написанной около 250 до н.э., Архимед показал, что это отношение ( $C/d$ , поскольку он не использовал обозначение $\pi$ ) больше 3, но меньше 3, вычислив периметры вписанного и описанного многоугольника с 96 сторонами[5]. Этот метод аппроксимации числа $\pi$ использовался столетиями, так как имел большую точность, нежели формулы многоугольников с большим числом сторон. Последнее такое вычисление производилось в 1630 году Кристоф Гринбергер[en], использовавшим многоугольники с 1040 сторонами.

Эллипс[править | править код]

Нет общей формулы для вычисления длины границы эллипса через большие и малые полуоси эллипса, которая бы использовала только элементарные функции. Однако, есть приближённые формулы, в которых фигурируют эти параметры. Одно из приближений получено Эйлером (1773); периметр эллипса, записанного каноническим уравнением:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,$

приблизительно равен

$C_{\rm {ellipse}}\sim \pi {\sqrt {2(a^{2}+b^{2})}}$

Нижние и верхние границы периметра канонического эллипса при $a\geq b$ [6].

$2\pi b\leqslant C\leqslant 2\pi a,$

$\pi (a+b)\leqslant C\leqslant 4(a+b),$

$4{\sqrt {a^{2}+b^{2}}}\leqslant C\leqslant \pi {\sqrt {2(a^{2}+b^{2})}}.$

Здесь верхняя граница $2\pi a$ — длина описанной концентричной окружности, проходящего через концевые точки больших осей эллипса, а нижняя граница $4{\sqrt {a^{2}+b^{2}}}$ — периметр вписанного ромба, вершины которого — концы больших и малых осей.

Периметр эллипса может быть описан с помощью полного эллиптического интеграла второго рода[7]. Более точно:

$C_{\rm {ellipse}}=4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta ,$

где — длина большой полуоси и — эксцентриситет ${\sqrt {1-b^{2}/a^{2}}}.$

См. также[править | править код]

Длина дуги
Изопериметрическое неравенство
Эллипс

Примечания[править | править код]

↑ Bennett, Jeffrey & Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (англ.) (3rd ed.), Addison-Wesley, с. 580, ISBN 978-0-321-22773-7
↑ San Diego State University. Perimeter, Area and Circumference. Addison-Wesley (2004). Дата обращения: 6 марта 2020. Архивировано из оригинала 6 октября 2014 года.
↑ Jacobs, Harold R. (1974), Geometry (англ.), W. H. Freeman and Co., с. 565, ISBN 0-7167-0456-0
↑ Sloane, N. J. A. Sequence A000796, On-Line Encyclopedia of Integer Sequences OEIS, OEIS Foundation.
↑ Katz, Victor J. (1998), A History of Mathematics / An Introduction (англ.) (2nd ed.), Addison-Wesley Longman, с. 109, ISBN 978-0-321-01618-8, <https://archive.org/details/historyofmathema00katz/page/109>
↑ Jameson, G.J.O. Inequalities for the perimeter of an ellipse (англ.) (англ.) // Mathematical Gazette (англ.) (рус. : journal. — 2014. — Vol. 98, no. 499. — P. 227—234. — doi:10.2307/3621497. — JSTOR 3621497.
↑ Almkvist, Gert & Berndt, Bruce (1988), Gauss, Landen, Ramanujan, the arithmetic-geometric mean, ellipses, pi, and the Ladies Diary (англ.), American Mathematical Monthly Т. 95 (7): 585–608, doi:10.2307/2323302, <https://semanticscholar.org/paper/8e3c462f5eb920fe178985f159cdfee815b59c52>

Литература[править | править код]

Атанасян Л. С., Бутузов В. Ф. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М.: Вита-Пресс, 2003.
Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 стр.

Ссылки[править | править код]

Numericana — Circumference of an ellipse

Как вычислить окружность?

Окружность — это геометрическая фигура, которая состоит из всех точек на плоскости, находящихся на одном и том же расстоянии от фиксированной точки, называемой центром окружности.

Для вычисления окружности нужно знать ее радиус (расстояние от центра окружности до любой точки на окружности) или диаметр (расстояние между двумя точками на окружности через ее центр).

Для вычисления окружности по радиусу нужно умножить диаметр на число π (пи), которое равно примерно 3,14 или 22/7.

Формула для вычисления окружности: C = 2πr, где С — длина окружности, r — радиус окружности, π — число пи (примерно 3,14).

Для примера, если радиус окружности равен 5 см, то ее длина будет C = 2πr = 2 * 3,14 * 5 = 31,4 см. Таким образом, длина окружности равна 31,4 см.

Вычисление длины окружности — основные аспекты и методы